画像をダウンロード 多項式 の 次数 162341-多項式の次数をテンソル積で表す

体論 生成元の取り替えと最小多項式 龍孫江 りゅうそんこう 可換環論botオペレーター Note
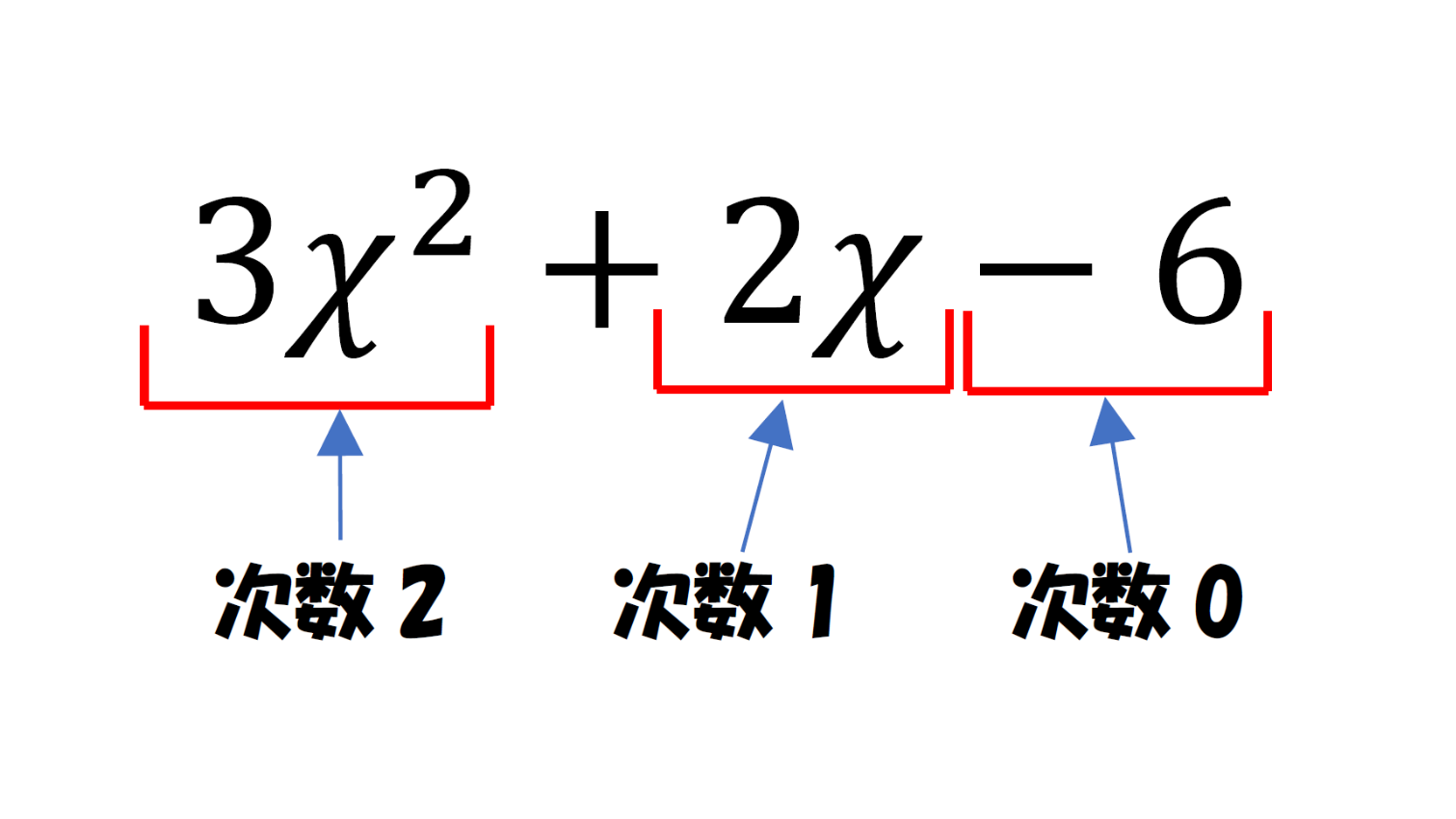
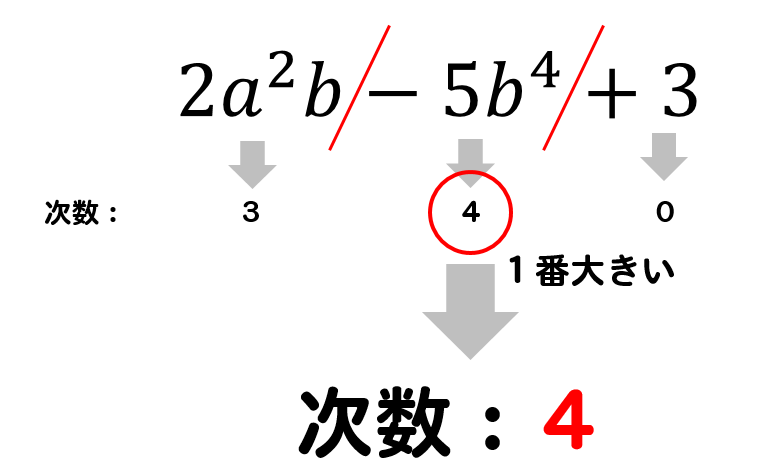
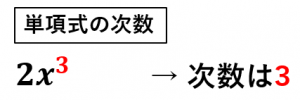
次数とは? 次数(じすう)とは、掛け合わせた文字の個数です。 例えば、 です。 累乗は指数の数が、次数になります。 また整式の項の次数で最大のものを、「整式の次数」といいます。 整式の意味は、下記が参考になります。 多項式とは? 1分で 単項式 前回、文字の解説をしたときに、数字と文字の間の \times 記号は省略できるという話をしました。 このように、数や文字、それらをかけ合わせて出来る式のことを 単項式 といいます。 単項式の数の部分を 係数 、文字の個数を 次数 といいます。 例えば、 3a の係数は 3 、次数
多項式の次数をテンソル積で表す
多項式の次数をテンソル積で表す-単項式の「和」として表されるものを多項式と定義するが, 2x 2 −4x3=2x 2 (−4)x3 のように,単項式の「差」で書かれるものも,符号を逆にした項の「和」と考えることができるから,単項式の差が含まれる式も,そのままの形で多項式という. 参考22 多項式とは、変数と定数から 足す引く掛けるだけの演算で 作ることができる式のこと。 √を使ったら、次数も何も 多項式の次数には、x の絶対値が小さいときの 式の値の小ささや、 x が大きいときの式の値の大きさを 概ね決めてしまう力があり、
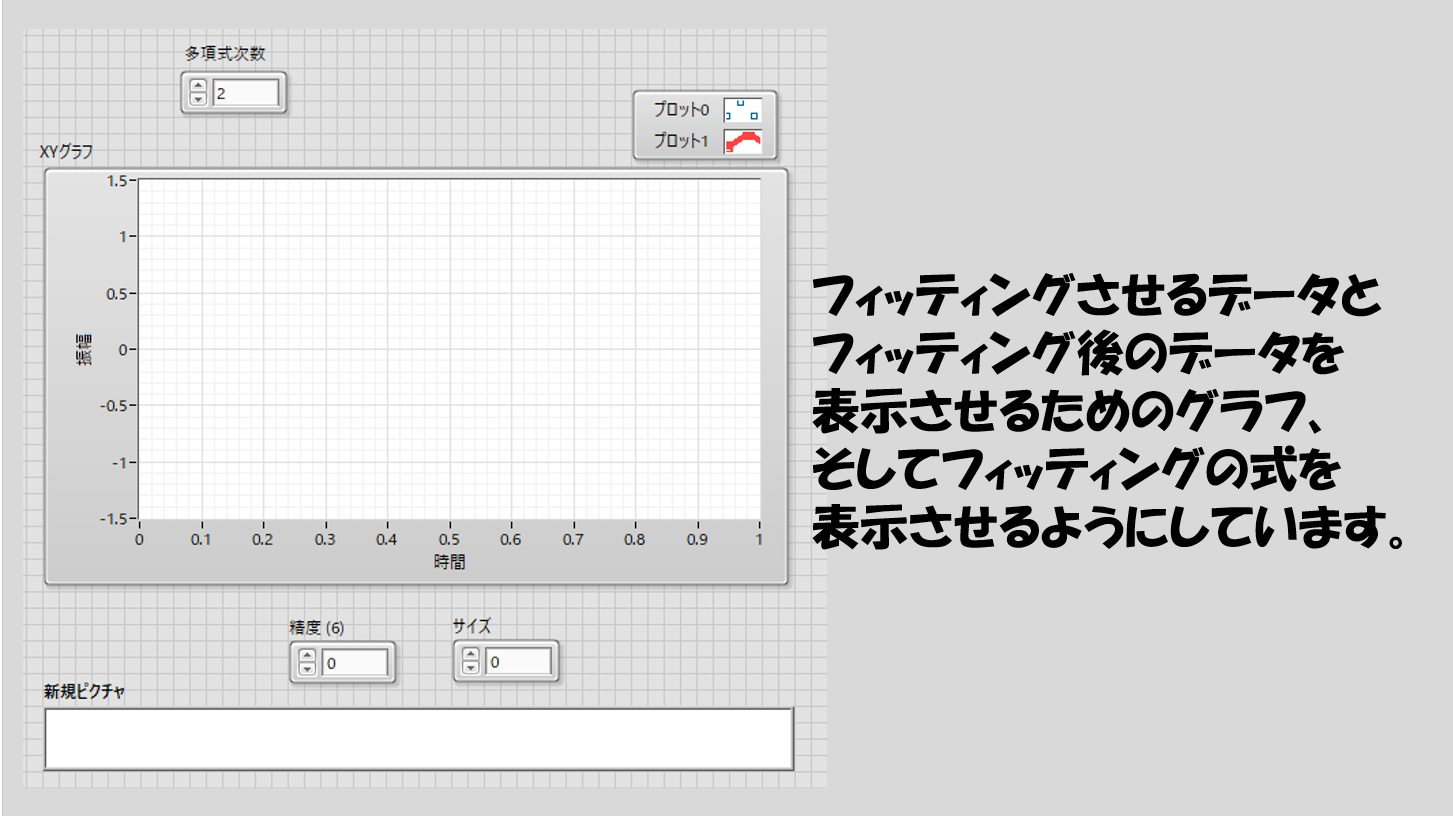
フィッティングの式を表示させる マーブルルール
符号多項式ですべての符号多項式を割り切り(の因数となり)、最小次数のものをその巡回符号の生成多項式という。 定理(構成法1) U を長さnの巡回符号とする。 u(x)=p(x)g(x) ( g(x):Uの生成多項式 ) が満たされることである。見れば今すぐわかる最小多項式 (体論)数学の分野である体論において、最小多項式(さいしょうたこうしき、)は体の拡大 と拡大体 の元に対して定義される。元の最小多項式は、存在すれば、 を変単項式の係数と次数 単項式の数の部分を係数といいます。ただし、 1x のように係数が 1 のときは省略して x と表されるので、 x の係数は 1 です。 同様にして、 −1a のように係数が −1 のときは省略して −a と表されるので、 −a の係数は −1 です。
多項式の割り算(まとめ) 準備 1. 割る式も割られる式も降べきの順に整理しておく. (必ず,次数の高い方から順に割ること) 2. 割られる式で,ない項はあけておく. (初め(係数が0で)空いていても,途中で登場するのが普通なのであけておかないと計算がもつれてしまう)進研ゼミからの回答 どのような順番で書いても間違いではありません。 でも,数学では次のように項を整理して書くことが一般的です。 ①わかりやすいようにアルファベット順に。 ②多項式の次数がすぐわかるように,次数の高い項の順に。多項式 多項式を調べ,定義域と値域,次数,根,プロット,判別式等の特性を計算する. 多項式の特性を計算する: x^4 4x^3 8x 1 複数の変数を持つ多項式の特性を計算する: x^3 x^2 y x y^2 y^3 多項式の次数を求める: (x2)^5 (x2)^5の次数 多項式の
多項式の次数をテンソル積で表すのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
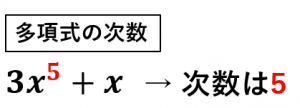 |  |  |
 |  | |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 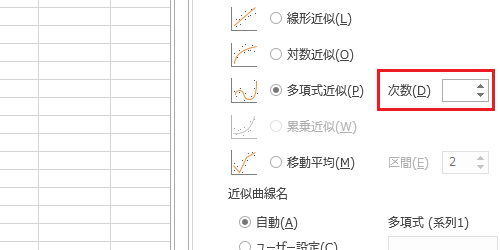 | |
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 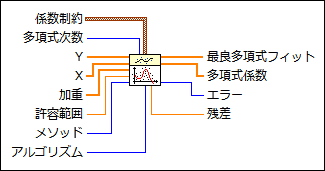 | |
 |  |  |
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
/GettyImages-183954354-57f140213df78c690fad23b7.jpg) |  |  |
 |  |  |
 | ||
「多項式の次数をテンソル積で表す」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
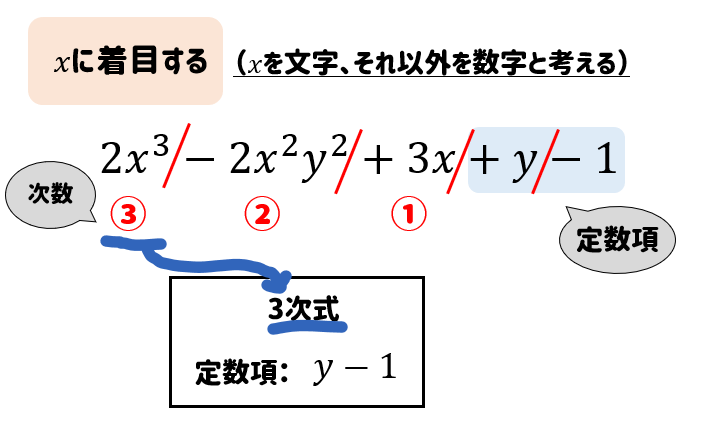
多項式についての用語の定義 多項式を構成しているそれぞれの単項式を 項 と呼びます。 多項式の各項の次数の中で,最も大きい次数を多項式の 次数 と言います。 さらに,数の部分のみからなる項は 定数項 と呼ばれます。 例えば, − 6 x 2 y 5 z x y 4・原始元を根とするような最小次数の多項式 g(x) を原始多項式と いう つま り x は原始元で g(x)=0 だから g(x) は原始 多項式になっているが、他の要素も原始元でありうるし、それに対する原始多項式が存在するということである。 n=4 ビットの例 で見て
Incoming Term: 多項式の次数, 多項式の次数とは, 多項式の次数と定数項, 多項式の次数の求め方, 多項式の次数の求め方 xに着目, 多項式の次数判別 エクセル, 多項式の次数をテンソル積で表す,
コメント
コメントを投稿